
It was hard to see my desk under the clutter of sticky notes. For years I worked in team rooms at Microsoft and relied on the ample supply of sticky notes in the supply room to organize my daily to-dos, in-progress work, weekly plans and future ideas. This was not a great organizational system, but the sticky notes were free and unlimited so why not? Over time, I adopted better practices to lessen my need for the plethora of paper but one use remained – self-reminders to combat anxiety.
I have fought with anxiety my whole life. When I began working professionally, I frequently left conversations or meetings feeling dismayed that my anxiety had taken control of my behavior. Eventually, I started using sticky notes to leave reminders on my monitor (often covering a small portion of the screen) to help interrupt the cycle of anxiety.
The messages were simple. Stay Calm. Take a breath. Slow Down. These didn’t magically solve how I felt, but they provided a moment of reflection to let my thinking brain back into the room. I did this for years, but I felt embarrassed about it since I wasn’t comfortable talking about anxiety. I hid the messages by abbreviating them so others wouldn’t know what I was doing when they saw letters S.C. stuck to my screen.
While I have a better hold of my anxiety than I used to, it remains a daily presence and I still use visual reminders (although not sticky notes) to shake me out of a spiral. Above my desk at home, I have a canvas print depicting Sisyphus pushing a boulder up a hill as a reminder that letting anxiety take control is a self-defeating process.

Let’s build something
It has been a long time since I even though about my sticky note days. But after a recent meeting where I felt frustrated over acting too much out of anxiety, the idea came back to me. Without the limitless supply of sticky notes, I decided to build an app (seemed like a good enough reason to learn the basics of Swift and Mac application development) to revisit the idea.
The concept was simple, a Mac OS app that allows pinning a customizable message to the menu bar that is always visible. I used this as an oppotuntiy to experiment writing software using Chat Oriented Programming (CHOP) with Sourcegraph’s Cody AI agent (disclaimer: I work at Sourcegraph).
Impressively, by describing my requirements and iterating on the resulting components, I created a working app quickly with 80% of the fuctionality. However, as it often is, that last 20% took the majority of the time. A couple behaviors and features required more research and reading to get working smoothly.
Handling Menu Bar Occlusions
My first pass used Swift UI to add the text to the Mac menu bar. Swift UI makes building UX components a breeze and I also used it for the settings dialog. But using it for the menu bar limited the ability to listen to occlusion status events. The Mac menu bar is a fickle friend that, depending on the screen size and other menu bar items, can evict your menu bar item at any moment. Reacting to eviction requires listening to events and adjusting the size. This meant leaving the comfort of Swift UI behind for rendering the menu bar and implementing those parts of the application as an application delegate. In the delegate, I attempted to render the full message and if it didn’t fit, render just an emoji. Making this work smoothly took a lot of trial and error.
Persistent Popover
To account for the full message not always being visible in the menu bar, I added a pinnable message popover to view the full message when you hover over the menu bar item. I first used the built-in popover component which is very convenient, but inflexible and dissapears when a user changes workspaces (virtual desktops). To make sure the pinned message always shows, I built custom popover component using a window component and view controller.
No more sticky notes
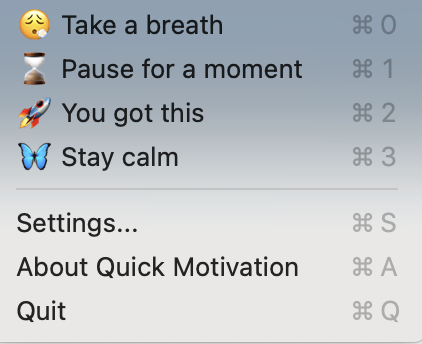
The end result is … Quick Motivation, a simple Mac app that adds a menu bar item with customizable messages.
Menu bar message

Quickly change between custom messages
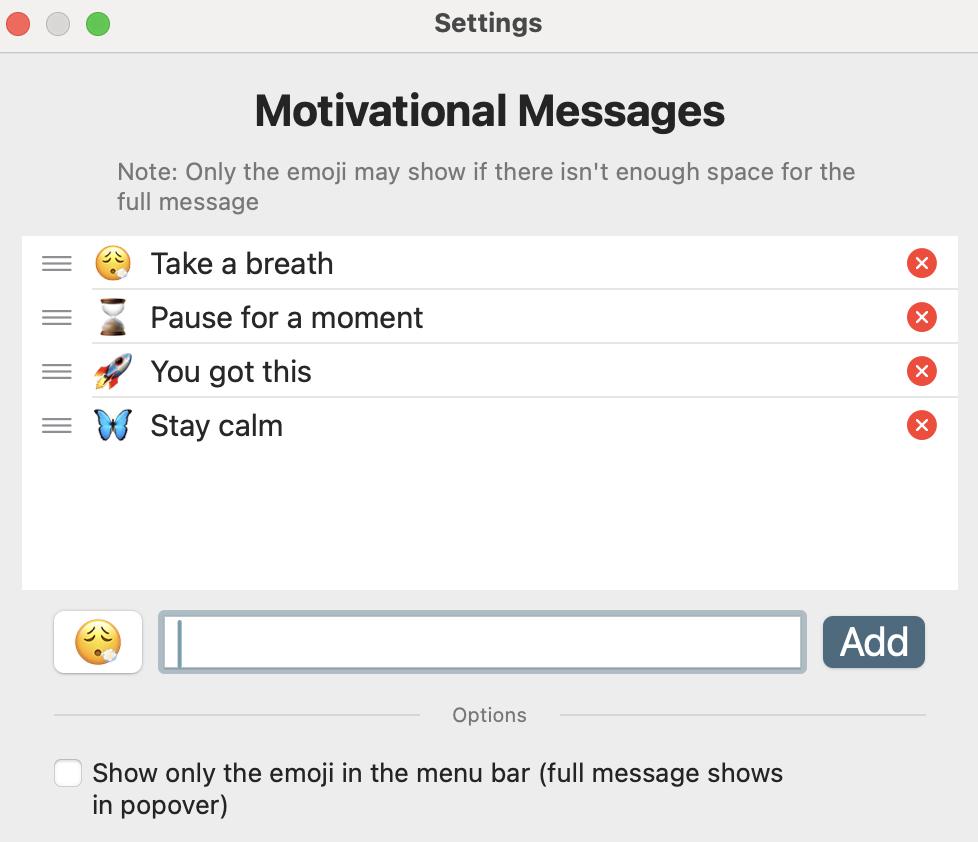
Configure new messages
Pin a message anywhere on the screen

You can install the app from the Mac App Store and view the source code on GitHub. While this is not a large or complex application, I learned a ton creating it and I hope others will find it useful.


